Er bestaat een getal dat eeuwenlang als bijna magisch wordt beschouwd. Kijk naar de rangschikking van zonnebloempitten of de vorm van een spiraalstelsel– telkens duikt Phi (φ) op. Of lijkt het op te duiken. Phi staat vooral bekend als de gulden snede en fascineert zowel kunstenaars als wetenschappers: het verbindt wiskunde met schoonheid en lijkt terug te keren in uiteenlopende patronen in de natuur. In dit tweede artikel over Phi (het eerste vind je via deze link) maken we een reis door tijd en ruimte – van de oude Grieken tot moderne kwantumfysica, van microscopische DNA-spiralen tot het spiraalvormige patroon van sterrenstelsels – om te onderzoeken of en hoe φ werkelijk de vingerafdruk van de natuur is.

Oude wortels van een mysterieus getal

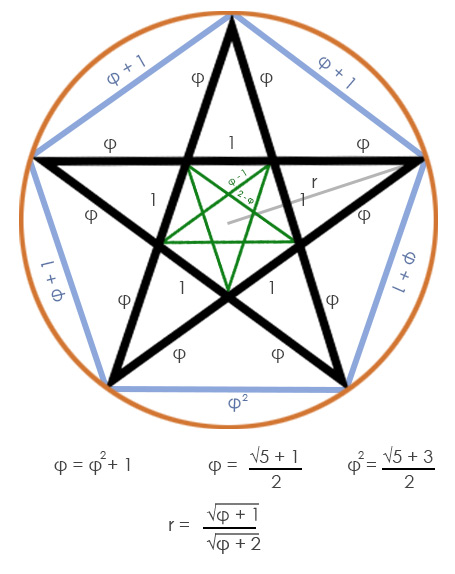
Het idee van een bijzondere verhouding was al bekend bij de oudst bekende wiskundigen. De Pythagoreeërs (6e eeuw v.Chr.) – volgelingen van de filosoof Pythagoras – verheerlijkten getallen en meetkundige vormen als de sleutels van het universum​. Hun geheime symbool was het pentagram. Dat is de vijfpuntige ster waarin verschillende lijnstukken elkaar precies in de gulden snede delen. Er is slechts één figuur die dat speciale fenomeen bevat. De Pythagoreeërs beschouwden het pentagram daarom als heilig: de verhoudingen in een regelmatige vijfhoek en pentagram zijn zonder uitzondering allemaal φ​. De verhouding werd in die tijd nog niet expliciet als Phi benoemd, maar de geometrische constructie was bekend.

Men wist (vermoedelijk) al veel langer van het bestaan af, maar de eerste gedocumenteerde beschrijving van de gulden snede vinden we bij Euclides van Alexandrië (~300 v.Chr.). In zijn invloedrijke werk Elementen definieerde hij het verdelen van een lijn in een “verhouding van het uiterste tot het middelste”. Euclides beschreef hiermee hoe je een lijnstuk zó in twee delen kunt opsplitsen dat de verhouding van het gehele lijnstuk tot het langste deel gelijk is aan de verhouding van het langste tot het kortste deel. Deze bijzondere verdeling vertaalt men naar de algebraïsche vergelijking x = (x + 1) / x. In mensentaal betekent deze formule: elk nieuw moment volgt uit de meest minimale vorm van groei, waarin alle mogelijke varianten verborgen zitten. Daarmee was Phi wiskundig gezien vastgelegd voor de eeuwigheid, zij het nog niet onder de naam Phi. Dat zou nog zo'n 2000 jaar duren.

In de renaissance dook Phi opnieuw op in de schijnwerpers. De Italiaanse monnik en wiskundige Luca Pacioli schreef in 1509 met het boek De Divina Proportione (“De goddelijke proportie”) een lofzang erover. In dezelfde tijdsperiode gebruikte Leonardo da Vinci de gulden snede in zijn tekeningen van het menselijk lichaam (waaronder de bekende Vitruviusman) om ideale proporties weer te geven. Daarover bestaat overigens discussie, want sceptici durven te beweren dat Da Vinci de magisch lijkende verhouding niet opzettelijk gebruikte. Hetzelfde zegt men over zijn Mona Lisa en ander werk. Onder ons gezegd en geschreven: Leonardo wist waar de klepel hing, want het net genoemde boek van Pacioli dat rijkelijk verhaalde over de wereld van Phi werd geïllustreerd door Da Vinci. In dat boek wordt de gulden snede verheerlijkt als een hemelse, esthetische verhouding die in de kunst en architectuur toegepast zou moeten worden en wordt Da Vinci door Pacioli uitdrukkelijk genoemd als hoofdbron van veel van de gebruikte wiskunde. De kans dat Leonardo de gulden snede niet bewust gebruikte lijkt daardoor klein.

Mede door boeken als Divina Properione groeide het mystieke aura rond Phi. Men noemde het de goddelijke verhouding, een scheppingsgetal verstopt in de natuur door de hand van God. Pas in 1835 kreeg het officieel de kortere naam goldener Schnitt van de Duitse wiskundige Martin Ohm. Dat liet zich snel naar het Nederlands vertalen als gouden/gulden snede. Golden ratio, in het Engels. Eindelijk een gemakkelijke naamgeving om dit fenomeen te vatten!

Spiraalvormige patronen in planten

De verhouding die Phi vertegenwoordigt is een eenheid binnenin de eenheid. Het is dan ook treffend dat de zaden (eenheden in een eenheid) van veel bloemenkoppen twee sets spiraallijnen vertonen: bijvoorbeeld 89 windingen linksom en 144 rechtsom, of een andere variant van opeenvolgende Fibonacci-getallen – een hint naar de gulden snede in de natuur. Planten demonstreren misschien wel het meest tastbare voorbeeld van φ in de natuur want ondanks dat het de gehele realiteit vormt lijkt het spel der verhoudingen over het algemeen geen blikvanger. Alle zaden in het hart van de zonnebloem zijn gerangschikt in spiraalpatronen die zowel met de klok mee als tegen de klok in draaien. Hoe meer zaden de zonnebloem bevolken, hoe dichter de verhouding tussen de twee spiralen Phi benadert. Dit is geen toeval. Het onderliggende mechanisme kreeg de wetenschappelijke naam fyllotaxis, dat is de manier waarop bladeren, bloemen en zaden groeien volgens een vast hoekverschil. 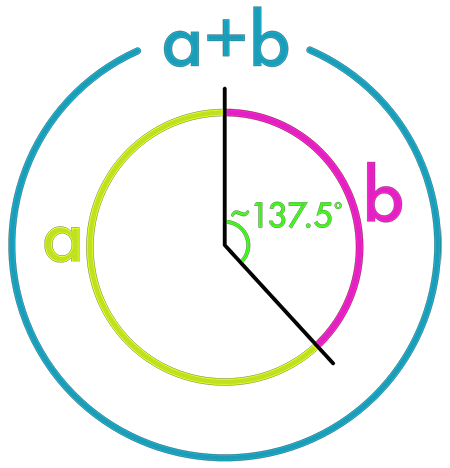Bij veel planten is die hoek ~137,5°, bekend als de gulden hoek. Deze hoek is direct afgeleid van φ: het is gelijk aan 360° × (1 – 1/φ) ≈ 137,5°.

Waarom precies die hoek? Het antwoord ligt in optimalisatie. Een plant wil nieuwe bladeren of zaden zo plaatsen dat ze elkaar minimaal overschaduwen. Puur praktisch. Als de groeipunten elke keer met de gulden hoek roteren, stapelen de organen zich (op) in een spiraal waarbij nooit twee bladeren precies boven elkaar komen. Dit komt doordat 137,5° een irrationele breuk van de cirkel is – in feite de meest irrationele, omdat φ het “minst benaderbare” irrationele getal is. Zou de plant bijvoorbeeld 120° of 144° kiezen, dan zouden bladeren na een paar omwentelingen weer in een lijn zitten, wat overlap geeft. Met 137,5° gebeurt dat niet: de positie schiet telkens langs de cirkel op, zonder ooit perfect te herhalen. Hierdoor ontstaat een prachtig spiraalpatroon dat een optimale verdeling van licht en ruimte biedt. Het resultaat van deze gulden-hoekstrategie zien we in talloze plantvormen. Zonnebloemen, madeliefjes, artisjokken, dennenappels, ananassen en zoveel meer – ze tonen allemaal twee reeksen spiralen waarbij het aantal spiralen vrijwel altijd Fibonacci-getallen zijn​. Zo heeft een dennenappel bijvoorbeeld 8 spiralen in de ene richting en 13 in de andere, en een ananas 5 en 8. Deze getallenparen (5, 8, 13, 21, 34, 55, 89, 144, ...) zijn Fibonacci-getallen. De deling van opeenvolgende Fibonacci-getallen schommelt rond 1,618 en benadert φ steeds nauwkeuriger.

De natuur “weet” natuurlijk niets van Fibonacci of φ af. Moeder Natuur heeft net zo min een telraam in haar schort verstopt als Vadertje Tijd een zonnewijzer om zijn pols heeft. Wat er werkelijk gebeurt is dat de gulden hoek een gevolg is van optimaal groei- en samenklitgedrag. De Fibonacci-verhoudingen volgen daar automatisch uit, als bewijs dat we in een prachtige in elkaar gewoven wereld leven.
Een bekende verschijning in die wondere wereld is de mooie romanesco. Deze groente smaakt bijna hetzelfde als een bloemkool en ziet eruit als een voedzame LSD-trip. Op de foto links zijn de typische fractal-achtige spiralen ervan mooi te zien. Een fractal is een zelfgelijkende structuur die zich kenmerkt door herhaling op verschillende groottes. Dat betekent dat wanneer je inzoomt op een deel, je een patroon terugziet dat lijkt op het oorspronkelijke geheel.
Er bevatten natuurlijk veel meer (lekkere) groenten en planten pentagrammen of logaritmische spiralen. Wie goed rondkijkt kan bijna overal patronen ontdekken die de diepere aard van de natuur kenbaar maken. Over het algemeen geldt: de gulden snede verschijnt in planten omdat het groeiprocessen stabiliseert en efficiënt maakt. Dat is een eenvoudige verklaring voor een ogenschijnlijk mysterieus verschijnsel, al geeft dit natuurlijk geen antwoord op waarom de natuur zichzelf opdeelt en -splitst. Dat Phi ontstaat uit de optimale verdeling van een groeiproces zegt eigenlijk helemaal niets over het groeiproces zelf. Het is bijvoorbeeld een wonderlijk gegeven dat onze mensensoort exact zoals een fractal evolueert. Al sinds ons begin: de ene mens uit de buik van de ander, via de moederschoot. Als we de wereld om ons heen even niet vanzelfsprekend nemen, is dat niet groots?

Van atoom, molecule, planeet tot menselijke lichaam en geest: alles in de natuur bestaat uit verhoudingen van druk of spanning. Het hele universum lijkt een spel van balanceren en reguleren van ontelbaar veel vormen van druk. Daarin, zo boven zo beneden, zitten veel groeipatronen die telkens opnieuw terugkomen. In de natuur lijkt het alsof er overal heimelijk wiskundige optimalisatie is toepast. Het geheel probeert zich zoveel mogelijk optimaal te verdelen en ieder onderdeel ervan kan daardoor niet anders dan op de goede locatie zijn.

Dierenrijk: van schelpen tot slakkenhuizen

Niet alleen planten, ook dieren vertonen structuren die met φ geassocieerd zijn. Kan natuurlijk weinig anders, want als phi maar iets te maken heeft met optimalisatie van groeiprocessen, dan zouden we sporen ervan moeten aantreffen bij zowel fauna als flora. Voorzichtigheid blijft geboden want associatie maakt natuurlijk nog geen feitelijke waarheid. Een klassiek voorbeeld is de schelp van de Nautilus – vaak te zien in biologieboeken als toonbeeld van een “gulden spiraal” in de natuur. Deze inktvis maakt een spiraalvormige kalkschelp met steeds grotere kamers. Prachtig om te zien! Op het eerste zicht lijkt elke volgende kamer een vaste factor groter dan de vorige, en velen dachten: aha, dat is de gulden snede! Maar naha, dat is niet de gulden snede...

De dwarsdoorsnede van een Nautilus-schelp toont inderdaad een logaritmische spiraalvorm – een vorm waarbij de schaal overal gelijkvormig blijft terwijl hij naar buiten toe groeit​. Qua ontwikkeling is dat erg handig: het dier kan groeien zonder van vorm te veranderen, door steeds grotere kamers aan te leggen. Maar is de groeiverhouding wel écht φ? De wiskundige Clement Falbo mat in 1999 geduldig talloze Nautilus-schelpen en vond groeiverhoudingen variërend van ~1,24 tot ~1,43 per kwartslag, gemiddeld rond 1,33. Dat ligt ver van de gulden 1,618. Met andere woorden: de Nautilus groeit niet als gulden-snedespiraal. Het is een veel voorkomende misvatting die van bron tot bron is overgeschreven, zonder dat iemand blijkbaar de moeite nam om een gouden spiraal eens echt op een schelp te leggen (want dan merk je al snel dat hij niet past)​. Dit leert ons een wijze les niet overal φ te willen zien, louter omdat het een mooi gedachte is. Ook al zou het groeipatroon overal in zitten, in de voor ons waarneembare vorm is de perfecte verdeling niet zo breed gezaaid als men zou kunnen willen.

Betekent dit dat dieren en hun vormen niets met φ te maken hebben? Zeker niet! Er zijn wel degelijk biologische spiralen en verhoudingen dicht bij de gulden snede want ook de dierenwereld houdt van optimale groei. Slakkenhuizen en andere schelpen volgen uiteenlopende logaritmische spiralen; sommige kunnen toevallig dichter bij φ zitten dan de Nautilus, andere verderaf. Hoorns en slagtanden van zoogdieren (bijv. de krullende hoorn van een Kudu-antilope of de slagtand van een olifant) groeien ook ongeveer logaritmisch​. Onderzoekers Boeyens en Thackeray noteerden dat de kromming van een olifantstand, net als de spiraal van een schelp, vaak een constante groeiverhouding rond 1,6 lijkt te hebben​. Het is lastig die getallen heel exact te krijgen bij levende organismen (die nooit zo perfect zijn als een wiskundige lijn), maar het idee is dat er vergelijkbare groeiprincipes aan het werk zijn. Zelfs in ons eigen lichaam duiken gulden verhoudingen op – of lijken ze op te duiken. Zo heeft de menselijke cochlea (het slakkenhuis in het binnenoor) een spiraalvormige structuur. Palaeontologen ontdekten in versteende cochlea’s van mensachtigen dat de verhouding rond de 1,6 ligt​. Sommige analyses suggereren een logaritmische spiraal dicht bij de gulden spiraal​.

Nog kleiner dan spiralen in ons binnenoor is de Stentor, een eencellig organisme dat zichzelf kan herstellen als het in twee wordt gesplitst. De Stentor trekt zijn voedsel binnen via samentrekkingen waardoor een draaiende Fibonacci-ring in zijn celstructuur ontstaat. Terug in de grote wereld zijn er populaire boeken die beweren dat allerlei lichaamsverhoudingen Phi zouden zijn. Bijvoorbeeld de verhouding tussen lengte tot navelhoogte, of tussen onderarm en hand of gezichtsverhoudingen). Wetenschappelijk gezien variëren zulke verhoudingen enorm per individu maar wanneer men gemiddeldes van populaties bekijkt, komen soms getallen rond 1,6 uit de bus. Het blijft lastig bepalen of dit betekenisvol is of niet. We dienen altijd rekening te houden met confirmation bias: wie overal φ wil zien, kan het bijna overal wel ergens ontdekken. Dat hoeft niet altijd terecht te zijn, maar zelfs met deze kanttekening kunnen we zeggen dat het streven naar de perfecte Phi (lees: de perfecte balans) in veel van de wereld om ons heen terug te vinden is.

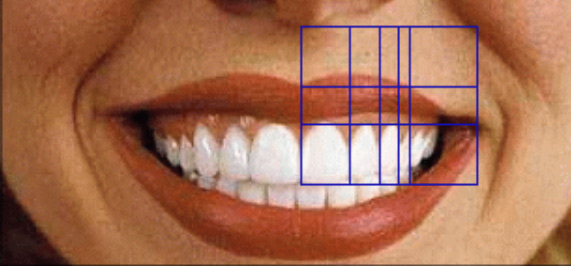De wereld om ons heen is zowel een eenheid als een verzameling van een breed scala aan groeiprocessen in groeiprocessen in groeiprocessen in. Sommige dingen groeien recht, andere krom. Onze tanden bijvoorbeeld. Tandartsen en orthodontisten gebruiken in hun werk regelmatig de gulden snede als richtlijn bij het ontwerpen van een esthetisch aantrekkelijke glimlach. Vooral de verhouding tussen de breedtes van de centrale en laterale bovensnijtanden benadert regelmatig de phi-verhouding. Zelfs als we met de mond vol tanden staan laat Phi zich ongemerkt zien.

φ op microschaal: DNA en kwantumverrassingen

We gaan nóg kleiner dan de Stentor en zoomen nu in op de microscopische wereld. Verrassend genoeg duikt φ ook hier op uiteenlopende plekken op – van de structuur van ons DNA tot exotische quantumverschijnselen. DNA – het bekende dubbele helix-molecuul dat onze genetische code draagt – lijkt een sterk staaltje natuur te zijn waar Fibonacci en φ mooi samenkomen. Experimentele metingen van de geometrie van de DNA-helix (de B-DNA vorm) tonen bijzondere getallen. Eén volledige winding van de dubbele helix, die 10 basenparen beslaat, is ongeveer 34 angström lang en 21 angström in diameter. Een angström (Å), genoemd naar Anders Jonas Ångström, is een lengtemaat van 0.1 nanometer. Dat is 0,0000001 millimeter. De angström wordt gebruikt om de afmetingen van atomen, moleculen en de afstanden tussen atomaire lagen in kristallen aan te geven.

Zowel 34 als 21 zijn Fibonacci-getallen en de verhouding ervan (~1,619​) schuurt opvallend dicht aan tegen φ. Bovendien heeft de DNA-helix een grote en een kleine groef die om elkaar heen draaien; de verhouding van de breedte van de grote groef tot de kleine groef is rond 21:13 angström – opnieuw getallen uit de Fibonacci-reeks, goed voor ~1,615​. Deze numerieke toevalligheden suggereren dat φ ingebakken zit in de spiraal van het leven. Natuurlijk dicteert de biochemie deze afmetingen (waterstofbruggen, basenpaarstructuren enz.), maar is het niet fascinerend te zien hoe de getallen zich verhouden? Hoe het leven hier zich verhoudt tussen de grenzen van geweest zijn en meer willen zijn dan het is?
Voor de duidelijkheid: natuurlijk is het niet zo dat DNA “kiest” voor φ. Simpel gezegd, het reageert perfect op veranderingen in zijn omgeving door zich optimaal aan te passen. Daarom is het niet zo heel opmerkelijk dat uit alle mogelijke moleculaire configuraties die de evolutie had kunnen gebruiken, ons erfelijk materiaal onderdelen heeft die deze speciale verhouding benaderen.

Naast biologie ontmoeten we φ ook in de vastestof- en kwantumfysica. In 2010 deden natuurkundigen een opzienbarende ontdekking: zij vonden de gulden snede terug in de quantuminformatie van een uiterst dun magnetisch kristal. Onderzoekers van de Helmholtz-Zentrum in Berlijn bestudeerden een nano-materiaal (cobaltniobaat) bestaande uit atomen in een lange ketting​. Bij zeer lage temperatuur en onder een precies afgesteld magnetisch veld ging die atoomketting over in een zogeheten quantumkritische toestand – een exotische toestand die als een soort fractaal beschouwd kan worden​. Wat ze vervolgens maten met neutronenverstrooiing, tartte de verbeelding: de energieniveaus van de trillingen in die atoomketting (denk aan de “toonhoogtes” van de magnetische golven) bleken in verhouding te staan tot elkaar als 1 : 1,618…​ Met andere woorden, de verhouding tussen de twee laagste excitatiefrequenties was φ, tot op hoge precisie. “Alsof de atomen zich gedragen als een nanoscopisch snaarinstrument dat zichzelf stemt volgens de gulden snede,” aldus de onderzoekers. 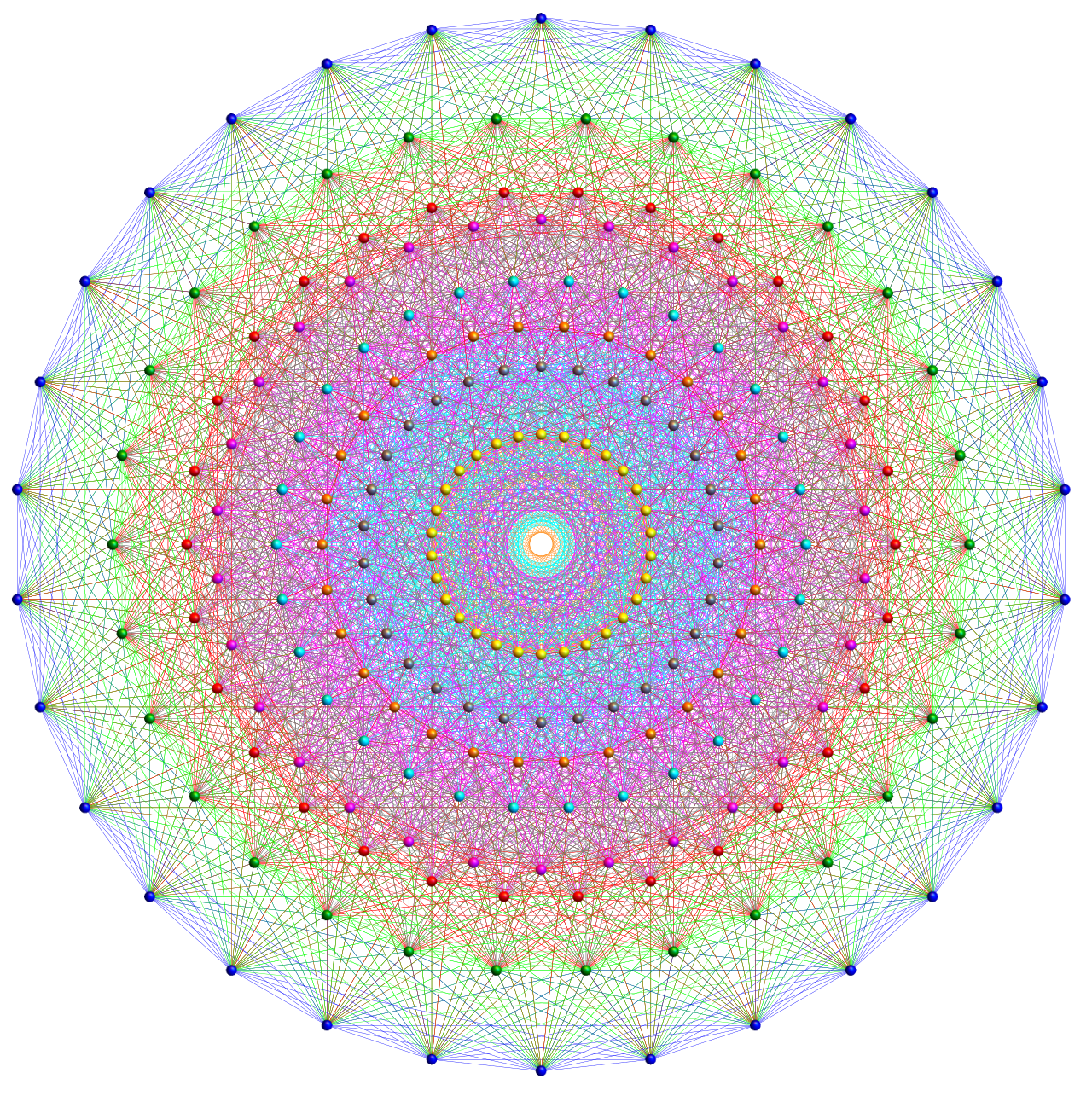Zij herkenden hierin een wiskundige symmetrie, namelijk de E8-symmetrie die nu voor het eerst experimenteel werd waargenomen in een materiaal​. Dit resultaat, gepubliceerd in Science, geeft aan dat φ geen toevallige schoonheid uit de kunstgeschiedenis is, maar een fundamentele symmetrie kan vertegenwoordigen die zelfs op atomaire schaal verschijnt.

Een ander voorbeeld op atoomschaal komt van de quasikristallen – vreemde kristallen met een quasi-periodieke structuur. Dat betekent dat er sprake is van een ordening die bijna, maar niet volledig regelmatig of periodiek is. In 1984 ontdekte Israëliër Dan Shechtman een legering met een vijfvoudige symmetrie, iets wat volgens de klassieke kristallografie onmogelijk was. Dit quasikristal bleek te bestaan uit atoomlagen die gerangschikt zijn volgens patronen die we kennen uit de Penrose-betegeling (mozaïek met aperiodieke stukjes), waarin Phi voortdurend opduikt. In zo'n quasikristal vinden we afstanden tussen atomen die in twee types voorkomen – laten we ze “kort” en “lang” noemen. De verhouding lang/kort blijkt overal ongeveer 1,618 te zijn. Dit komt direct voort uit de vijfvoudige symmetrie: elke regelmatige vijfhoek heeft diagonalen en zijden in gulden-verhouding, en dat principe zet zich voort in het hele quasikristal. Wetenschappers gebruiken zelfs de Fibonacci-reeks en Phi om de diffractiepatronen van quasikristallen te verklaren​. In 2011 kreeg Shechtman de Nobelprijs voor Chemie voor deze phintastiche ontdekking. In zijn toespraak benadrukte hij dat “de gouden verhouding telkens weer opduikt” als het sleutelaspect van quasikristalstructuren​. Phi is dus écht een bouwsteen van materie: het bepaalt direct hoe atomen zich positioneren in een stabiele maar niet-periodieke stapeling. Dit is een verbluffende link tussen pure meetkunde en de fysische realiteit van materialen. Een bewijs dat de wereld om ons heen een soort van verdeelmachine is die telkens dieper en dieper zichzelf in zichzelf verdeelt.

Phi op macroschaal: van planeten tot sterrenstelsels

We verlaten de nanometers en betreden de uitgestrektheid van het heelal. Zouden we Phi ook duidelijk kunnen bespeuren op macroniveau, bijvoorbeeld in de ordening van planeten, in de vorm van orkanen of misschien zelfs in sterrenstelsels? Er zijn inderdaad aanwijzingen en nog meer suggestieve patronen te ontdekken. Ons zonnestelsel toont enkele numerieke toevalligheden die met Phi in verband zijn gebracht. Zo is de verhouding tussen de baanstraal van planeet Venus en die van de Aarde ongeveer 0,723. Dit getal is interessant, want het is (bijna) 1/φ² (omgerekend ~0,382 is φ-1, dus 1/φ² ≈ 0,382, en omgekeerd φ² ≈ 2,618 wat dichtbij de Mars/Aarde afstandsverhouding ligt). Sommige onderzoekers hebben gewezen op een “gulden driehoek” gevormd door de afmetingen van de Aarde en de afstand tot de Maan: trek je een lijn vanuit het middelpunt van de Aarde naar dat van de Maan, dan vormt die lijn samen met de aardstraal een driehoek waarvan de zijden zich verhouden als 1 : √φ : φ​. Dit klinkt indrukwekkend, maar men moet beseffen dat planetaire afstanden door veel factoren bepaald worden en kleine variaties veel uitmaken – het is de vraag of dit meer is dan toeval of een leuke benadering. Wie het weet mag het zeggen...

Wél duidelijker is het voorbeeld van spiraalvormige fenomenen zoals orkanen en melkwegstelsels. Zowel een orkaan (bijv. de beruchte orkaan Katrina of Typhoon Tip) als een spiraalstelsel (bijv. ons Melkwegstelsel of het Whirlpool-stelsel M51) hebben de vorm van een logaritmische spiraal. Vaak worden afbeeldingen van zulke spiralen overlapt met een gulden spiraal (zoals geconstrueerd uit gulden rechthoeken) om te zien of ze overeenkomen. In sommige gevallen lijken de armen van een sterrenstelsel inderdaad grofweg de helling van een gulden spiraal te volgen, in andere gevallen niet. Wetenschappers die honderden sterrenstelsels hebben gemeten, vinden dat elk spiraalstelsel zijn eigen logaritmische spiraalhoek heeft, variërend van ongeveer 10° tot 40° afhankelijk van type – er is niet één universele waarde​. De gulden spiraal zou overeenkomen met een specifieke hellingsgraad (ongeveer 17° tussen elke 90° rotatie, samenhangend met factor 1,618 per kwartslag)​. De meeste sterrenstelsels wijken daar aanzienlijk van af; onze eigen Melkweg heeft bijvoorbeeld een gemiddelde spiraalhelling van rond de 12° (dus langgerekter). Kortom, de natuur kent talloze logaritmische spiralen, maar slechts zelden zien we de “gulden” variant​. Dat kan zijn omdat Phi een haast nooit bereikt natuurlijk streven is; dat kan ook zijn omdat Phi slechts 1 van de vele te verkrijgen verhoudingen is en toevallig een lading wiskundige eigenaardigheden aan zich heeft hangen.

De reden dat logaritmische spiralen überhaupt zo vaak voorkomen – van slakkenhuis tot sterrenstelsel – is dat ze zelfgelijkend groeien: de vorm blijft gelijk onder schaalvergroting, ideaal voor groeiprocessen en rotatiedynamiek. Phi is slechts één van oneindig veel mogelijke groeifactoren van zo’n spiraal, en er is geen fundamentele reden dat een orkaan juist die waarde “kiest”​. Toch spreken de beelden tot de verbeelding. Wanneer we een gulden spiraal over de foto van een kolkende storm leggen en zien dat hij bijna past, voelen we intuïtief een soort orde in de chaos – zelfs al weten we rationeel dat het niet exact is. Aan de andere kant hoeft het ook helemaal niet exact te zijn: het bestaan van φ illustreert juist dat we leven in een wereld die niet draait om één perfecte verhouding, maar eerder als een gevoelige weegschaal telkens opnieuw het hele spectrum van mogelijke verhoudingen verkent en gebruikt. In die subtiele variatie toont de natuur haar vermogen om te balanceren tussen orde en vrijheid, voorspelbaarheid en spontaniteit.

Misschien wel het meest intrigerende macroniveau-voorbeeld van φ komt van de sterren zelf. In 2014 ontdekten astronomen merkwaardig gedrag bij bepaalde pulserende sterren (RR Lyrae-variabelen). Ze analyseerden het geflikker van een dubbel-pulserende ster met behulp van de Kepler ruimtetelescoop. Een dubbel-pulserende ster is een ster met twee verschillende trillingsfrequenties die gelijktijdig plaatsvinden, waardoor interessante en complexe helderheidspatronen ontstaan. De wetenschappers vonden dat twee van de dominante pulsatiefrequenties zich verhouden als ~1,58​. Dat is verdacht dicht bij φ (1,618). Deze sterren vertoonden zogeheten “strange nonchaotic” gedrag: complexe, fractale patronen in hun variabiliteit, maar toch zonder de gevoeligheid voor begincondities die echte chaos kenmerkt​. Met andere woorden: te regelmatig om chaotisch te zijn, te chaotisch om de regelmaat in te herkennen.
Omdat de frequentieverhouding zo dicht bij de gulden snede zat, werden ze gekscherend “gouden sterren” genoemd​. De onderzoekers benadrukten dat de term gouden hier simpelweg beschrijvend is voor de verhouding, maar het roept natuurlijk de vraag op waarom juist die verhouding opdook. Mogelijk zorgen niet-lineaire resonanties in de ster ervoor dat bepaalde frequenties zichzelf “uitmiddelen” tot een irrationele verhouding en φ is daarbij het verst weg van welke simpele breuk ook. Men zegt soms dat Phi de “minst rationale” verhouding is omdat het van alle irrationele getallen het moeilijkst te benaderen valt met een breuk (een verhouding van twee gehele getallen). Dit zou stabiliserend kunnen werken, vergelijkbaar met de gulden hoek bij planten. Deze ontdekking is nog vers en er wordt vervolgonderzoek gedaan. Maar de gedachte dat zelfs in de ritmiek van sterren een echo van Phi klinkt, prikkelt de verbeelding.

Tot slot zijn er theoretische natuurkundigen die Phi proberen te koppelen aan de fundamenten van het universum. Zo suggereerde het wetenschappelijke duo Boeyens en Thackeray in 2014 dat φ een rol speelt in de topologie van de ruimtetijd zelf. Zij wijzen op overeenkomsten tussen Phi en allerlei natuurconstanten en biologische constanten, en speculeren over een “unificatie” waarin φ als soort kosmische constante fungeert. Dit zijn gewaagde ideeën aan de frontlijn van wetenschap en filosofie. De mainstream fysica heeft Phi (nog) niet erkend als fundamentele constante zoals de lichtsnelheid of de zwaartekrachtsconstante. Toch is het opmerkelijk dat φ op zoveel schalen en plaatsen opduikt, van de structuur van het periodiek systeem der elementen tot verhoudingen in kosmologische modellen​.

Reflectie: toeval, evolutie of fundament?

We hebben de gulden snede ontmoet in bladeren, bloemen, in stentors, slakkenhuizen en DNA en misschien zelfs in de kwantumtoestand van alle materie. In deel 1 van deze artikelreeks opperden we zelfs de mogelijkheid dat de reeks van Fibonacci sinds de Babylonische tijd aan de basis kan liggen van onze moderne 60-delige tijdsregistratie. Hoe kunnen we deze omnipresentie van Phi duiden? Is de gulden snede een soort verborgen code van de natuur, een signatuur van schoonheid en efficiëntie die de kosmos doordringt? Of is het vooral onze menselijke geest die er een rode draad in ziet, een hersenvirus gevoed door enkele spectaculaire voorbeelden en een eeuwenlange fascinatie? We vonden talloze concrete voorbeelden waar φ of bijna-φ in de natuur opduikt. De gulden hoek bij planten maximaliseert lichtopvang en zaadverdeling – een resultaat van evolutie en natuurkunde. De mystiek van dat scenario ligt in de waarom iets zich telkens opnieuw optimaal verdeelt en niet zozeer in het patroon dat er logischerwijs uit volgt. Het ontstaan van Phi is een gevolg van optimalisatie, niet de oorzaak ervan. In quasikristallen vloeit φ voort uit de wiskunde van vijfvoudige symmetrie; logischerwijs verschijnen die verhoudingen dan in atoomafstanden​ als het levende pentagrammen.

Phi manifesteert zich in DNA via de Fibonacci-reeks vanwege de geometrische structuur van de dubbele helix. Er zijn vele voorbeelden die tonen dat de natuur soms lokaal φ “uitzondert” omdat het de meest stabiele of efficiënte oplossing biedt voor een probleem – niet anders dan hoe de natuur π (pi) gebruikt in cirkelvormige structuren of e (de constante van Euler ~2,718) in groeiprocessen. Anderzijds is er de onbeantwoorde vraag: waarom zijn deze fundamentele verhoudingen überhaupt zo vaak fraai irrationeel? Het is frappant dat uitgerekend Phi – de “mooie” verhouding die de mens al eeuwen esthetisch en intellectueel boeit – zich manifesteert op zoveel niveaus. Onthult het iets over hoe ons universum in elkaar zit? Sommige wetenschappers en filosofen neigen naar het idee dat wiskunde de onderliggende taal van de natuur is, en dat bepaalde getalsverhoudingen onvermijdelijk opduiken zodra systemen complex worden. In chaostheorie ziet men bijvoorbeeld ook terugkerende getallen, zoals Feigenbaum-constanten. Misschien treedt Phi op als dimensieloze constante, bepalend voor de structuur van oplossingen, omdat ze inherent verbonden is met de kern van hun ontstaan.

Phi is een sleutel in begrijpen hoe het éne zich splitst en kan blijven splitsen tot en voorbij de wereld zoals we die kunnen zien. Maar die gulden sleutel is geen gouden loper die op elk koperen slot past. Als het op getallen en betekenis aankomt blijft waakzaamheid voor de doorgewinterde denker geboden. Het zien van φ betekent niet dat φ bewust “gekozen” is door de natuur of de artiest. Tenzij misschien in het humoristische geval van φφ doet ππ...
Phi ontstaat als een gevolg van hoe de natuur werkt: groeiend (door te delen) van binnenuit naar buiten op zo'n manier dat ieder atoom zich precies bevindt waar het moet zijn, anders zou het daar niet eens kunnen zijn. Alles in harmonie met de omgeving. Net zoals een gezonde foetus groeit in de buik van de moeder en zelden in een kartonnen doos ernaast, zo is ieder deel op de goede plaats. Dat φ om ons heen terug te vinden is toont (samen met heel veel andere zaken) dat onze realiteit een soort van doorlopende verdeelmachine is waar licht op wordt geworpen. Ieder moment in ons leven wordt gesplitst in alle mogelijkheden van elk nieuwe moment.

Phi is geen alomvattende code die alles stuurt, maar zeker ook geen triviale curiositeit. Het is een brug tussen wiskunde en natuur, tussen fysica en metafysica, tussen zijn en willen zijn. Bij fenomenen die de eigenschappen van zelfgelijkheid, optimale verdeling of vijfvoudige symmetrie bezitten zien we Phi vaak opduiken. Dit maakt het tot een soort universalia – een natuurlijk terugkerend motief, vergelijkbaar met hoe hexagonale structuren (zoals bijenraten en basaltkolommen) telkens opduiken als optimale stapelmethode in 2D. En net zoals we in een honingraat zowel esthetiek als functionaliteit zien, zo kunnen we φ bewonderen om zijn schoonheid én begrijpen vanuit de wiskundige wetenschap.

De gulden snede blijft boeien omdat ze op een uniek snijpunt ligt van natuur en cultuur. Het inspireerde kunstenaars (en tandartsen) van de oudheid tot nu. Zelfs in onze tijd duiken er steeds vernieuwende wetenschappelijke ontdekkingen op die de intrigerende verhouding een plek geven, bijvoorbeeld de resonanties in een quantumspin-keten. Af en toe zien we de gulden glans van een diep in het systeem gewortelde orde (zoals φ en π) te midden van het dagdagelijkse ogenschijnlijke toeval en de eindeloos veel andere verhoudingen waarin ons universum de realiteit verdeelt. Daarvan gesproken, in deel 3 van deze Phi-reeks verkennen we occulte gebieden en analyseren we het duivelse pentagram zó grondig dat het bijna Pentametrie wordt...