Wanneer we 's ochtends onze ogen openen, bevinden we ons altijd ergens. Iedere dag ontwaken we in een wereld waarvan we weten dat hij in grote lijnen dezelfde is als gisteren. We rekenen op patronen: dat de zon weer opkomt, onze handen elk vijf vingers hebben, en dat de wereld zich laat herkennen via herhalingen en regelmaat. Maar wat als achter die vertrouwde patronen een verborgen verband schuilt, een mysterieuze verhouding die zich overal openbaart? Van de spiralen in sterrenstelsels tot de precieze ordening van zaadjes in een zonnebloem, van de proporties van ons lichaam tot de diepere structuren in kunst en architectuur – telkens blijkt één bijzondere verhouding aanwezig te zijn. Die verhouding heet Phi (φ), beter bekend als de gulden snede. Maar waarom?

In dit eerste artikel van een fascinerende reeks duiken we diep in Phi: we onderzoeken wat het precies is, waarom het keer op keer opduikt in de natuur, en hoe deze verhouding een bijzondere brug slaat tussen orde en chaos. Ook verkennen we hoe Phi eeuwenlang filosofen, kunstenaars en wetenschappers inspireerde, en waarom sommigen vermoeden dat deze verhouding zelfs een sleutel kan zijn tot begrip van bewustzijn en een verborgen ritme in de kosmische klok van het universum.

Nieuwsgierig geworden naar de diepere verbanden achter alles wat je ziet? Laat je meenemen op een ontdekkingsreis door mystieke geheimen, intrigerende patronen en eenheid achter verscheidenheid.

Phi: de universele verhouding die het Ene trouw blijft in verdeling

Eén is één en dat betekent dat, als het aankomt op verbonden zijn met iets, één nergens mee verbonden is (tenzij dan misschien met alles). Vol of leeg, het is niets meer dan zichzelf. Pas bij de allereerste deling van (én in) de eenheid, hoe dat er ook uit moge hebben gezien, ontstond er iets niet-zichzelf, iets anders. Bij die eerste deling ontstond naast de nieuw gevormde onderdelen automatisch de allereerste verhouding. Meer is een verhouding niet: hoe twee onderdelen zich tegenover elkaar schikken. Daarom zijn er oneindig veel verhoudingen mogelijk, maar er is één verhouding, één manier waarop de natuur zich deelt, die zó speciaal is dat het de hele natuur kan bevatten.

Misschien handig om te weten dat de getalswaarde van Phi (φ) afgerond 1,61803 is. Afgerond, want ná de komma gaat het getal eindeloos verder. Wiskundigen noemen zo'n rusteloos getal irrationaal. Niet dat die 1,618 als getal eigenlijk zo belangrijk is, verre van. Phi is voornamelijk speciaal omwille van hoe de onderdelen zich verhouden ten opzichte van elkaar. Maar laat je niet afschrikken door het abstracte karakter: we kijken samen stap voor stap naar wat Phi praktisch betekent in de wereld om ons heen.

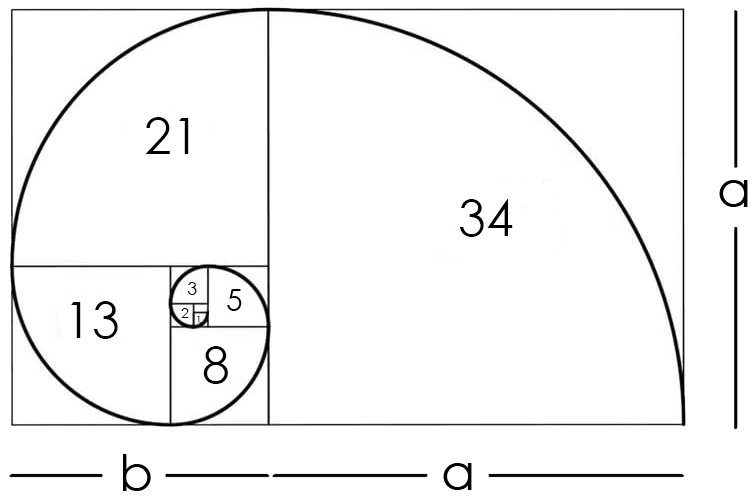
Phi ontstaat wanneer iets zich op een heel specifieke manier splitst of opdeelt. Dat iets kan letterlijk van alles zijn. Neem bijvoorbeeld een stuk touw en verdeel het in twee delen. Als je zorgt dat de verhouding van het kortste deel (b) ten opzichte van het langere deel (a) hetzelfde is als de verhouding van het langste gedeelte met het geheel, dan heb je de gulden snede toegepast. In wiskundige woorden schrijft men dit als: (a + b) : a = a : b = φ.

Er zijn nog meer elegante formules die tonen hoe speciaal Phi is en aangeven dat er een eenheid mee gemoeid is. De vergelijking φ² = φ + 1 is daar eentje van. We zullen er meer aantreffen doorheen de artikelreeks. Het idee dat “het geheel zich verhoudt tot het grotere deel zoals het grotere zich verhoudt tot het kleinere” betekent dat er een zelfgelijkenis optreedt – de verhouding blijft hetzelfde, ongeacht of je naar het grote geheel kijkt of naar een kleiner onderdeel. Ongeacht de schaal. Daarom omschrijven oude geschriften de mens als evenbeeld van God. Niet het letterlijke spiegelbeeld (want God valt niet in een enkel beeld te bevatten omdat hij geen spiegel heeft maar een spiegel is) maar eerder een gemeenschappelijke verhouding in (bewust)zijn. Het Ene (het geheel) wordt als het ware getrouw gespiegeld in de delen ervan. Dit is waar men op doelt met “de universele verhouding die het Ene trouw blijft in verdeling”: zelfs wanneer je een geheel opsplitst, behoudt deze specifieke verhouding de harmonie tussen deel en geheel. Er is slechts één verhouding met deze goddelijke eenheidsharmonie: Phi.

Phi wordt al eeuwenlang bewonderd vanwege deze zelfgelijkende eigenschap. Euclides, de Griekse wiskundige die leefde rond 300 voor Christus, beschreef het in de Oudheid als het verdelen van een lijn in “extreme en gemiddelde verhouding”​. De 17e-eeuwse astronoom Johannes Kepler (die ons leerde hoe de planeten rond de zon bewegen) noemde de gulden snede zelfs een “kostbaar juweel van de meetkunde”​. Grote woorden die werden uitgesproken omdat hij wist hoe bijzonder het was dat een enkel getal zo’n elegante samenhang in zich draagt.
Filosofisch gezien biedt de spiegel-eigenschap van Phi een prachtige metafoor: het Éne (eenheid, het geheel) en het vele (de steeds dieper gaande delen) zijn niet volkomen gescheiden, maar weerspiegelen elkaar in harmonie en ontwikkeling. Alsof er een soort verborgen orde is waardoor elk deel de stempel van het grote geheel draagt. Alsof iedere vooruitgang in het teken staat van willen zijn zoals de bron, maar dan meer of voller. Als een puzzel met schijnbaar oneindig veel verschillende puzzelstukjes terwijl in feite telkens hetzelfde puzzelstukje nét iets anders wordt neergelegd. Dit principe van één in velen resoneert met oude wijsheden die stellen dat de werkelijkheid een onderliggende eenheid bevat. Phi levert hier een tastbaar, visueel voorbeeld van: de delen blijven het Ene trouw in hun onderlinge verhouding. Of met meer moderne woorden: het éne wordt op vele manieren gesimuleerd. Dit fenomeen kunnen we met het blote oog zien. En als dat al zichtbaar is, wat vertelt dat ons dan over de onzichtbare structuren achter de werkelijkheid zelf?

Phi verschijnt via de Fibonacci-reeks

Om de gulden snede beter te doorgronden kunnen we kijken naar de beroemde Fibonacci-reeks waar φ een soort kloppend hart van is. Die reeks is eenvoudig opgebouwd. Iedereen die met plus kan werken kan de reeks eenvoudig zelf samenstellen. Wel een blad papier en pen erbij nemen, want de getallen worden snel groot.
Om de Fibonacci-reeks te maken beginnen we met tellen vanaf 0 om daarna naar 1 gaan. Ieder volgend getal is dan de som van de twee voorgaande. Dus bij 0 + 1 wordt de volgende 1. Nu de reeks 0, 1, 1 is kunnen we de volgende in de rij bepalen door 1 en 1 samen te tellen, wat 2 is. Dan 2 + 1 = 3, dan 2 + 3 = 5 en zo gaan we door en krijgen we de reeks 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... enzovoort​.

Op het eerste gezicht lijken deze getallen niets met Phi te maken te hebben, maar als je opeenvolgende Fibonacci-getallen deelt dan begint er iets opmerkelijks te gebeuren. Neem bijvoorbeeld 5 en 3 (opeenvolgend in de reeks): 5/3 ≈ 1,667; neem 8 en 5: 8/5 = 1,6; neem 13 en 8: 13/8 = 1,625; bij 21/13 ≈ 1,615; 34/21 ≈ 1,619; 55/34 ≈ 1,6176. Deze quotiënten gaan ergens naartoe: ze naderen steeds dichter φ.
Als je deze delingen blijft doen met steeds hogere Fibonacci-getallen, zul je uiteindelijk de waarde van Phi benaderen tot op willekeurig veel decimalen nauwkeurig. Hoe hoger de getallen (dus hoe meer data of informatie er beschikbaar is) hoe duidelijker de verhouding zich aftekent. Dit is geen toeval, Johannes Kepler – dezelfde die Phi het “kostbaar juweel” noemde – merkte al op dat de Fibonacci-reeks en de gulden snede onlosmakelijk verbonden zijn. Zo’n inzicht toont dat Phi diepgeworteld zit in de structuur van eenvoudige reeksen en telpatronen.

Phi toont zich ook via een ander prachtig ontvouwend patroon. Links is de driehoek van Pascal geanimeerd te zien. De vorm is genoemd naar de Franse denker Blaise Pascal (1623–1662) naar wie in meer moderne tijden zelfs nog een computerprogrammeertaal werd genoemd.
Blaise was geïnteresseerd geraakt in het aantal mogelijke combinaties waarmee men bijvoorbeeld dobbelstenen kan werpen of muntjes kan gooien. Hij wilde berekenen hoe vaak iets zich voordeed en daar hielpen zijn studies naar waarschijnlijkheid, combinaties en kansberekeningen goed bij. Ongeveer zo (her)ontdekte Blaise het dieper gelegen patroon in de 17e eeuw. Zoekend naar het perfecte dobbelspel construeerde de Fransman een driehoek waarin elk getal ontstaat uit de optelsom van de twee bovenliggende. Ligt er geen getal links- of rechtsboven dan rekenen we nul. Het is simpelweg opsplitsen, gewoonweg delen, net zoals bij de reeks van Fibonacci maar anders. Dat verdelen is een belangrijk concept want ondanks de schijnbare complexiteit in de wereld om ons heen kunnen we uiteindelijk stellig zeggen: Moeder Natuur snijdt alles in twee. Of was het den duivel die alles wat wij zien verleidelijk verdeelde? Het woord "diabolisch" komt immers van het Latijnse diabolicus en oorspronkelijk van het Griekse diabolos. Het betekent letterlijk "Hij die dingen uit elkaar werpt" of "Hij die verdeelt". Een interessant gegeven om later dieper op in te gaan.

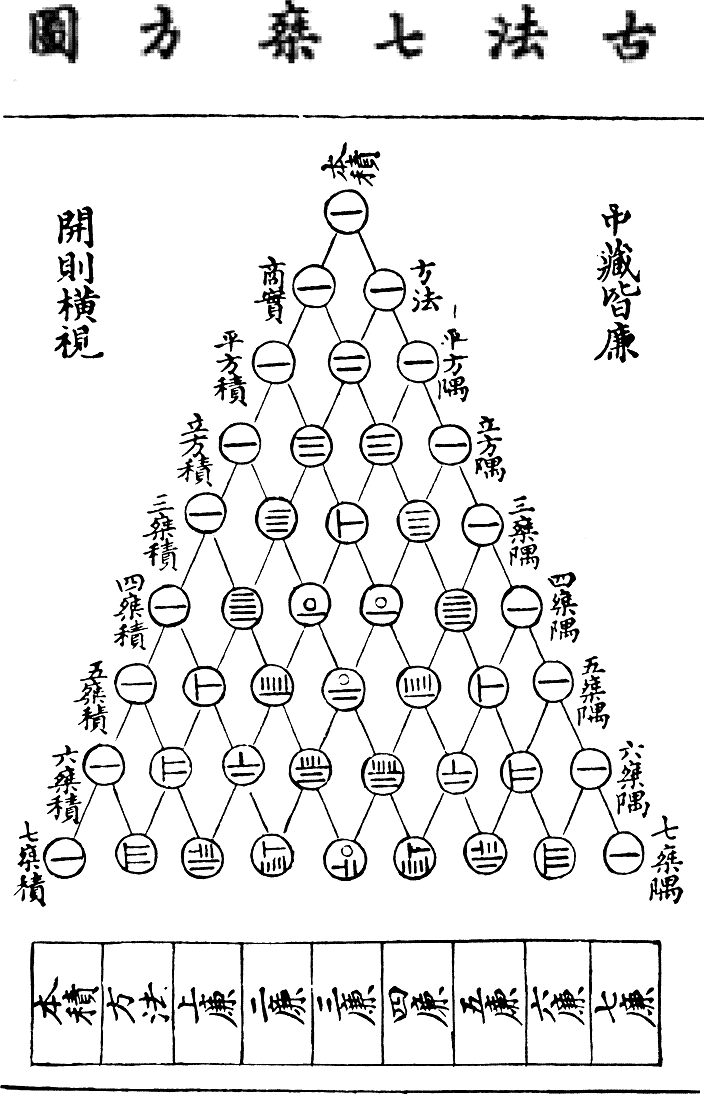
Eeuwen voordat Pascal met zijn driehoeken aan het spelen was kende men dit patroon reeds in andere culturen. In India noemde men het de “trappenberg van Meru”. In oude Indiase literatuur wordt de “trappenberg van Meru” vaak als metafoor gebruikt. Dichters beschrijven de opbouw van de heilige berg als symbool voor de spirituele reis, waarin elke trap staat voor een stap richting verlichting. Bij de bouw van heilige tempels werd de structuur van de trappenberg gebruikt om de kosmische orde te weerspiegelen.
Ook in het oude China dook deze driehoek al op als de Yang Hui-driehoek die men gebruikte om problemen op te lossen over hoe je dingen op verschillende manieren kunt combineren en ordenen. Chinese landbouwers en handelaren gebruikten de principes van de driehoek om bijvoorbeeld te bepalen op hoeveel manieren goederen konden worden verdeeld over verschillende groepen of hoe zaden optimaal over een oppervlak geplaatst konden worden.
Eveneens in het Midden-Oosten werd rond de 11e eeuw door de Perzische geleerde Omar Khayyám de driehoek toegepast bij het oplossen van algebraïsche vergelijkingen. Kortom: krachtig rekengereedschap. De verdienste van Blaise Pascal ligt vooral in het blootleggen en benadrukken van de diepgaande verbanden die deze eenvoudige driehoek met talloze andere mathematische fenomenen verbindt — waaronder de gulden snede. Zo verbindt dit ogenschijnlijk simpele combinatiespel verschillende culturen en eeuwenlange inzichten met elkaar in een prachtige en betekenisvolle symmetrie. Over de hele wereld is met bezig met hetzelfde: zoeken naar de verborgen eenheid.

Waarom is dat belangrijk? Omdat de Fibonacci-reeks niet slechts een spelletje van getallen is. Phi (of het streven ernaar) is een onderdeel van het wereldse bouwplan waar wijzelf een onderdeel van zijn. Dat de mysterieuze verhouding opduikt in de natuur is een eerste hint dat de gulden snede meer is dan wiskundige nieuwsgierigheid. Bijvoorbeeld, het aantal bloemblaadjes van veel bloemen is een Fibonacci-getal. Ook de manier waarop de spiralen van zonnebloempitten of dennenappelschubben zich verhouden volgt de gulden snede, telkens paren van Fibonacci-getallen: een bepaald aantal spiralen met de klok mee en een ander aantal ertegenin​. Dat zorgt ervoor dat de hoek tussen opeenvolgende zaden in de zonnebloem een gouden hoek is, gerelateerd aan de gulden snede, waardoor de zaden optimaal worden verpakt zonder overlap. "Optimaal" is hierbij het trefwoord. Phi is de optimale manier waarop iets zich in volledige volheid kan verhouden ten opzichte van iets anders.

Belangrijk om te melden is dat Phi vermoedelijk nergens in de natuur exact aangetroffen wordt. Net zoals er in de natuur geen perfecte cirkels te vinden zijn (en dat terwijl érg veel natuurkundige fenomenen Pi (3,1415...) bevatten), zo bevat de perfecte verhouding Phi altijd een streven naar verdere verdieping en is daardoor per definitie altijd benaderend en nooit volmaakt. Phi is (net als Pi) een irrationaal getal, wat betekent dat het oneindig lang doorgaat na de komma. Het stopt niet met deelbaar zijn. Als men dus ergens Phi in ontdekt dan is dit in de meeste gevallen een benadering en niet de volledige precieze waarde of verhouding, zelfs al gebruikt men Fibonacci-getallen zoals bij de zonnebloemverhoudingen.

Met Phi’s wiskundige fundamenten in gedachten – een uniek irrationaal getal dat voldoet aan φ² = φ + 1 en dat verschijnt in de limiet van eenvoudige telrijtjes – kunnen we nu verkennen hoe deze “universele verhouding” zichtbaar wordt in de werkelijkheid om ons heen. Hoe vertaalt die abstracte verhouding zich naar spiralen, patronen en misschien zelfs bewustzijn?

Phi als brug tussen orde en chaos

Eén van de meest fascinerende aspecten van Phi (naast dat het een universele sleutel lijkt te zijn) is hoe het tevoorschijn komt in situaties die balans vragen tussen regelmaat en variatie – met andere woorden, tussen orde en wanorde. In de natuur zien we talloze structuren die niet perfect symmetrisch of herhalend zijn (dat zou te ordelijk zijn), maar ook niet totaal willekeurig (chaotisch). Denk aan de verdeling van bladeren rondom een tak, de schikking van zaadjes in het hart van een zonnebloem, of de spiraalvorm van een pijnboompitstructuur. Deze patronen moeten efficiënt zijn: bladeren willen maximaal zonlicht opvangen zonder elkaar te veel te overschaduwen, en zaden moeten zo compact mogelijk groeien zonder elkaar te verdringen. De natuur heeft hiervoor een slimme oplossing: een hoek en verhouding gebaseerd op de gulden snede.

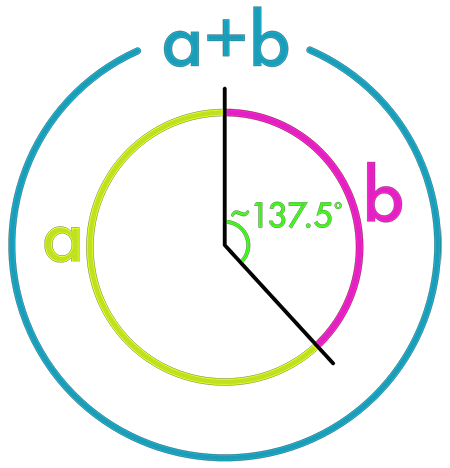Bij zonnebloemen bijvoorbeeld worden nieuwe zaadjes telkens onder een hoek van ongeveer 137,5° ten opzichte van het vorige geplaatst. Deze hoek staat bekend als de gouden hoek, omdat hij voortkomt uit de gulden snede (het is gerelateerd aan 360° * (1 – 1/φ)). Het resultaat is een prachtig spiraalpatroon waarbij de zaden in twee sets spiralen liggen – doorgaans een set van bijvoorbeeld 34 spiralen linksom en 55 rechtsom, of 21 en 34, etc., Fibonacci-getallen dus. Hierdoor ontstaat geen dominante structuur die tot rijen (en dus ongebruikte ruimte) leidt, maar ook geen ongestructureerde wirwar. Het patroon oogt organisch en quasi-willekeurig, maar heeft onder de oppervlakte een strakke wiskundige regelmaat. Dit is Phi in actie als brug tussen orde en chaos: de gulden snede levert een verhouding die nooit in een eenvoudig getallenbreuk is te vangen (het is één van de meest irrationele getallen die er zijn), en daardoor zullen structuren gebaseerd op φ zich nooit exact herhalen als een kristalrooster (te veel orde), maar ze zijn wel overal consistent genoeg om stabiliteit en efficiëntie te bieden (geen pure chaos).

We zien een vergelijkbaar principe bij zogeheten quasi-kristallen en aperiodieke patronen, zoals de beroemde betegeling gemaakt door de slimme Brit Roger Penrose. Zijn Penrose-betegelingen zijn patronen die geen regelmatige herhaling hebben (zoals een regulier vloerpatroon dat wel heeft), maar toch een onderliggend ordeprincipe volgen. Interessant genoeg duikt φ ook in deze context op: de verhoudingen van afstanden in Penrose-patronen zijn bijvoorbeeld gebaseerd op de gulden snede. Het resultaat zijn mozaïeken die nooit twee keer hetzelfde stukje patroon hebben, en toch volledig in elkaar passen zonder gaten – wederom die balans tussen regelmaat en verrassing.

Op een grotere schaal duikt Phi zelfs op in de wereld van chaostheorie en dynamische systemen. Zo is de gulden snede verwant aan wat men de “gouden verhouding” in frequenties noemt: als twee trillingen of cycli een frequentieverhouding van φ hebben, zullen ze nooit in exact dezelfde fase terugkeren en zo ontstaat een soort quasi-periodische dynamiek. In de complexe systemen aan de rand van chaos kan φ daardoor verschijnen als stabiele verhouding die net voorkomt dat het systeem volledig periodiek of juist volledig chaotisch wordt.

Een eenvoudige illustratie hiervan is muziek: twee tonen waarvan de frequenties zich als een eenvoudige breuk verhouden (bijv. 2:1 of 3:2) geven consonante, repetitieve klankinterferenties (orde), terwijl volstrekt niet-gerelateerde frequenties dissonante ruis kunnen geven (chaos). Een verhouding als φ levert geen herhalende patronen op in de tijd, wat een rijke, volle harmonische samensmelting kan geven die tussen consonant en dissonant in zit – sommige componisten en wetenschappers experimenteren dan ook met de gulden snede in muziek.

Phi’s rol als brug tussen orde en chaos wordt ook mooi verwoord door de wetenschap achter evolutie van planten. Een studie aan de Universiteit van Cambridge toonde aan dat de Fibonacci-patronen in planten (en dus indirect de gulden snede) een gevolg zijn van evolutionaire optimalisatie: het zijn patronen die zorgen voor maximale blootstelling en efficiënte benutting van ruimte en middelen​. Met andere woorden, de natuur “probeert” allerlei mogelijkheden en de patronen die noch te stijf geordend, noch te rommelig chaotisch zijn, blijken het succesvolst. Phi markeert precies die grens waar orde en variatie elkaar perfect in evenwicht houden.

Phi en bewustzijn: eenheid, schoonheid en esoterische inzichten

De alomtegenwoordigheid van Phi in de natuur en wiskunde roept een intrigerende vraag op: is het louter toeval of wijst het op iets fundamenteler – misschien zelfs iets dat met bewustzijn of waarneming te maken heeft? Filosofen, kunstenaars en esoterici hebben door de eeuwen heen gefascineerd naar de gulden snede gekeken als een mogelijke sleutel tot verborgen kennis. Maar op welke sloten past Phi dan precies?

Allereerst is er het aspect van schoonheid en esthetiek. Mensen ervaren vormen die de gulden snede benaderen vaak als aangenaam en in harmonie. Of het nu de verhoudingen van een klassiek gebouw zijn, een schilderij van Da Vinci of de indeling van een foto, composities op basis van φ worden als natuurlijk en prettig ervaren. Sommigen suggereren dat dit komt doordat ons bewustzijn of ons brein als het ware resoneert met deze verhouding. Ons oog en brein houden van patronen die niet te simpel en saai zijn, maar ook niet te chaotisch – en dat is precies wat φ biedt, zoals we zagen bij orde en chaos. Het lijkt alsof ons bewustzijn zichzelf herkent in patronen gebaseerd op de gulden snede, omdat het misschien volgens vergelijkbare principes georganiseerd is. Er zijn theorieën in de neurowetenschap die bijvoorbeeld speculeren dat hersengolven of de connectiviteitsnetwerken in de hersenen fractale of schaal-invariante eigenschappen hebben (eigenschappen die onafhankelijk zijn van omvang en schaal), waarbij de gulden snede een rol zou kunnen spelen in optimale informatieverwerking. Hoewel dit onderzoeksgebied zeker nog in ontwikkeling is, past het idee in een bredere filosofische kijk: dat bewustzijn geen losstaand fenomeen is, maar verankerd ligt in de structuren van de natuur.

Wat ook moet worden gezegd: het mag dan zo zijn dat sommige mensen vormen gebaseerd op de gulden snede esthetisch aangenaam vinden, onderzoek toont niet aan dat dit effect universeel is. Mensen prefereren niet consequent φ boven andere verhoudingen. Niet iedereen verdeelt zijn leven in volledigheid áls er al mensen zijn die dit überhaupt doen.

Esoterische tradities gaan nog een stap verder. In de Hermetische filosofie, geïnspireerd door de oude leringen van Hermes Trismegistos, bestaat het axioma: “Zo boven, zo beneden; zo binnen, zo buiten.” Dit duidt erop dat de microkosmos (het kleinste) en de macrokosmos (het grootste) elkaar spiegelen en dat alles met alles verbonden is. Interessant genoeg wordt de gulden snede vaak gezien als illustratie van dit principe​. We zagen immers dat φ er precies voor zorgt dat het kleinere deel dezelfde verhouding tot het grotere heeft als het grotere tot het geheel – zo binnen, zo buiten. Het verschijnen van φ in zowel een bloem als een melkwegstelsel​, zowel in het molecuul DNA als in de verhoudingen van het menselijk lichaam, wordt door esoterici gezien als bewijs van een onderliggende eenheidsstructuur van de schepping. Alsof de “vingerafdruk” van de scheppende intelligentie overal terug te vinden is als dezelfde verhouding.

Los van complexe theorieën voelen veel mensen intuïtief iets “dieps” bij Phi. Bijvoorbeeld bij het zien van een perfecte logaritmische spiraal (die direct verbonden is aan φ) in een schelp of een zonnebloem, ervaren we vaak ontzag en een soort esthetische rilling. Het is alsof we een glimp opvangen van een groter geheel, een ordening waar wij zelf deel van uitmaken. Bewustzijn – ons vermogen om patronen te herkennen en betekenis te geven – lijkt als het ware afgestemd op deze gulden-snede-patronen. Misschien is dat omdat onze eigen fysieke vorm en natuurlijke omgeving ermee doordrenkt zijn, of misschien (zo zou een meer spiritueel georiënteerd mens zeggen) omdat ons bewustzijn ontspruit uit diezelfde universele orde.

In de oudheid werden dit soort kennis en inzichten vaak in geheimzinnigheid gehuld. Phi werd niet altijd expliciet benoemd, maar we zien wel dat bijvoorbeeld het pentagram, waarin de gulden snede meerdere malen voorkomt, een symbool was van de Pythagorese mysterie-school. Het pentagram was voor hen een teken van gezondheid en verbondenheid en werd soms geheim gehouden voor buitenstaanders – wellicht omdat het de sleutel tot de gulden snede bevatte, die destijds een bijna magische ontdekking was (het inzicht in irrationele verhoudingen)​. Het bewustzijn van de mens werd verondersteld zich te kunnen afstemmen op kosmische verhoudingen en ritmes, en Phi werd gezien als één van die belangrijke ritmes. Zo zijn er esoterische scholen (zoals in de heilige geometrie) die meditaties of visualisaties doen met de gulden snede vormen – denk aan een mentale constructie van steeds groter wordende golden rectangles of spiralen – in de hoop de geest te verenigen met de universele harmonie.

Hoewel de directe wetenschappelijke koppeling tussen Phi en menselijk bewustzijn moeilijk meetbaar is, blijft de symbolische connectie krachtig. Phi vertegenwoordigt harmonie en groei. Bewustzijn zoekt van nature naar harmonie en groeit in begrip. In die zin zou je poëtisch kunnen stellen dat Phi een blauwdruk van de kosmische geest is – een getalsmatige uitdrukking van hoe de ene bron (het Ene) zich in de veelheid van vormen uitdrukt zonder de verbinding te verliezen. Tenminste, dát is de gedachtegang die we terugzien in filosofische en esoterische bespiegelingen over dit bijzondere getal.

Phi in de oudheid: geheime kennis en toepassingen

De gulden snede fascineert de moderne mens, maar ze bleef ook in de oudheid niet onopgemerkt. Hoewel men in verschillende beschavingen niet noodzakelijk de notatie φ gebruikte of de exacte decimale waarde kende, zijn er aanwijzingen dat de verhouding op intuïtieve of empirische wijze toegepast en begrepen werd – soms openlijk, soms als geheime kennis binnen gesloten kringen. Sommige van deze kennis werd bewust geheim gehouden, juist omdat Phi als heilig of mysterieus werd beschouwd.

In het Oude Egypte bijvoorbeeld zijn er theorieën dat de piramidebouwers van Gizeh de gulden snede in hun ontwerp verwerkten. De Grote Piramide van Cheops heeft een hoogte en basisafmeting waarbij de verhouding tussen de schuine zijde (de oprijzing van de piramide) en de helft van de basis bijna exact φ is​. De piramide heeft een hoogte van 146 meter en een basisbreedte van 230 meter. De verhouding tussen de halve basisbreedte en de hoogte is 115/146 ≈ 0,7877. Deze waarde ligt dicht bij √Φ ≈ 0,78615, wat suggereert dat de piramide is ontworpen met de gulden snede in gedachten. Daarnaast vormt een dwarsdoorsnede van de piramide een driehoek van Kepler, met zijden in de verhouding 1 : √Φ : Φ. Hoewel we niet met zekerheid weten of dit doelbewust gebeurde, is het aannemelijk dat de bouwers kennis hadden van bijzondere wiskundige relaties. De Griekse historicus Herodotus suggereerde reeds dat de Egyptenaren beschikten over bijzondere wiskundige kennis in hun architectuur. Moderne berekeningen tonen in elk geval dat deze verhouding 1,618 (binnen 0,1% nauwkeurigheid) benaderd wordt in de geometrie van het antieke bouwwerk.

Ook de oude Grieken kenden de gulden snede, zij het onder andere namen. Pythagoras en zijn volgelingen, de Pythagoreeërs, waren berucht om hun bijna religieuze toewijding aan getallen en verhoudingen. Er is overgeleverd dat zij het bestaan van irrationele getallen (zoals φ) aanvankelijk geheim hielden, omdat het hun wereldbeeld van “alles is getal” op zijn kop zette.
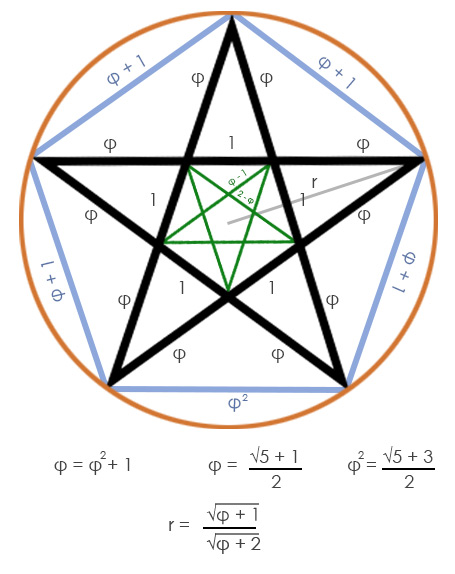
De ontdekking dat de diagonaal en de zijde van een pentagram zich via de gulden snede verhouden was voor sommigen een schokkende openbaring. Niet voor niets voerden de Pythagoreeërs een pentagram (wat vol zit met gulden snede verhoudingen in de lijnen) als soort van geheime handdruk-herkenningsteken onder elkaar​. Het pentagram gold als symbool van gezondheid en innerlijke harmonie.
Interessant is de verbinding met de planeet Venus: elke 8 jaar vormt de positie van Venus ten opzichte van de aarde een pentagram-patroon aan de hemel (het beroemde pentagram van Venus), aangezien Venus in 8 aardse jaren ongeveer 13 keer om de zon draait, een verhouding van 13:8 die dicht bij φ ligt​. De Pythagoreeërs zouden Venus gelijkgesteld hebben aan het pentagram​, wellicht beseffend dat hier een kosmische gulden greep zichtbaar werd. De cyclus van Venus weerspiegelde zich in de harmonie op Aarde (het pentagram als symbool van het menselijke microkosmos) – een prachtig “zo boven, zo beneden”-principe. Al is deze verhouding natuurlijk niet exact Phi, maar een benadering (zoals vaker bij kleinere Fibonacci-getallen).

Griekse architectuur en kunst maakte ook gebruik van harmonische verhoudingen. Hoewel het niet onomstreden is of de gulden snede bewust is toegepast in bijvoorbeeld het Parthenon, zijn de proporties van dat tempelgebouw en andere klassiekers vaak zodanig dat ze dicht bij φ-verhoudingen liggen, naast eenvoudige verhoudingen als 2:3. Sommige historici vermoeden dat de Grieken eerder gevoel volgden voor esthetische balans, wat automatisch tot φ-achtige verhoudingen kan leiden, dan dat ze berekend φ invoerden. Hoe dan ook, later in de Renaissance werd de “Divina Proportione” – de goddelijke proportie – zoals Luca Pacioli φ noemde, expliciet verheerlijkt in de kunst. Leonardo da Vinci illustreerde Pacioli’s werk en paste de sectio aurea (zo betitelden ze de gulden snede) toe in zijn schilderijen. Dit was geen toeval: Renaissance geleerden geloofden dat deze proportie een geheim van schoonheid was, overgeleverd vanuit de oudheid, en dat het bijna magische of goddelijke eigenschappen had. Het was “geheime” kennis in die zin dat het niet algemeen begrepen werd waarom deze verhouding zo’n effect had, maar ingewijden in de kunst en wetenschap herkenden het als signatuur van volmaaktheid.

In andere culturen vinden we soortgelijke benaderingen. In de Indiase en islamitische geometrische patronen bijvoorbeeld (zoals rangoli’s of girih-tegels) zie je vaak vijfhoeken, decagonale sterren en andere vormen waarin φ verstopt zit. Men zag deze geometrische patronen als meditatie over de orde van het universum – een manier om via visuele muziek dichter bij goddelijke eenheid te komen. Kabbalistische tradities en middeleeuwse mystici spraken soms in versluierde termen over het metend begrijpen van Gods schepping – wie weet verwezen sommigen daarbij ook naar de gulden maat. Het valt lastig te ontkennen dat alles relatief is, dus alles in verhouding staat tot...

Al met al was Phi in de oudheid zowel praktisch toegepast – in bouwkunst, verhoudingen van instrumenten, kalenders (sommige astronomische cycli benaderden φ-verhoudingen) – als symbolisch omarmd als sleutelfragment van de grotere kennispuzzel. Een mooi voorbeeld om dit af te ronden: De dodecaëder, één van de vijf Platonische lichamen, heeft twaalf vijfhoekige vlakken. In die vijfhoeken zit overal de gulden snede (de diagonalen van een vijfhoek verdelen elkaar in φ-verhouding). Plato koppelde de dodecaëder aan het gehele universum (in Timaeus suggereert hij dat de maker van de wereld deze vorm gebruikte voor de kosmos). Dat betekent dat voor de ouden de gulden snede – verborgen in de dodecaëder – geassocieerd was met het bouwplan van het universum zelf. Geen wonder dat latere generaties alchemisten en vrijmetselaars deze vorm en zijn proporties als geheime kennis beschouwden, iets om alleen aan de "waardigen" door te geven. Phi is als een gouden draad die door verschillende esoterische tradities loopt, glanzend genoeg om op te vallen, maar subtiel genoeg om mysterie te behouden.

Phi en de ‘kosmische klok’

Eén van de fascinerendste aspecten van Phi is hoe het zich manifesteert als een verborgen ritme achter cycli en patronen. Er wordt weleens gesproken van een “kosmische klok”: het idee dat het universum bepaalde ritmes volgt, met perioden die resoneren op verschillende niveaus—zoals dag en nacht, seizoenen, planetaire cycli en galactische bewegingen. Zou het kunnen dat Phi, als fundamentele groeiverhouding, ook betrokken is bij zulke tijdcycli? Het lijkt haast niet anders te kunnen...

We noemden al het voorbeeld van de cyclus van Venus en de aarde: 8 jaar op aarde komt dicht bij 13 jaar op Venus, waardoor het patroon van ontmoetingen een pentagram vormt. De getallen 8 en 13 zijn Fibonacci-getallen en hun verhouding is ongeveer 1,625, opvallend dicht bij φ (1,618)​. Dit is mogelijk meer dan een kosmisch toeval: twee planeten die een relatief stabiele dans uitvoeren die gerelateerd is aan de gulden snede. Voor sommige oude culturen, zoals de Maya’s, was de cyclus van Venus heilig en fungeerde het als een soort kalender. Men zou kunnen zeggen dat Venus en Aarde samen een kleinere klok vormen binnen de grotere kosmische klok, met Phi als de verhouding tussen hun tandwielen.

Het concept van de kosmische klok kan ook metaforisch worden begrepen. Stel je de tijd voor als een spiraal in plaats van een cirkel. Geschiedenis herhaalt zich nooit precies, maar vertoont wel overeenkomsten op hogere spiralen van ontwikkeling. Geschiedenis rijmt, noemt men dat. Een cirkel zou pure herhaling zijn (terug bij af na elke omloop), maar een logaritmische spiraal – en de gouden spiraal is daar een speciaal geval van – groeit elke omwenteling een vast percentage. Als de tijd in gulden snede zou “groeien”, zou elke cyclus 1,618 keer groter zijn dan de vorige. Of misschien wel 1,618 keer zoveel gebeurtenissen als iedere vorige tijdsperiode. Dit idee duikt op in spirituele leringen die spreken over versnelling van bewustzijn of evolutie, of in new-age theorieën waar men denkt dat gebeurtenissen op grotere schaal resoneren met kleinere schaal events via fractal-achtige timing. Hoewel niet wetenschappelijk bewezen (noch gemakkelijk te bewijzen), heeft het beeld kracht: de gulden spiraal als tijdspad betekent dat er wel ritmes zijn (spiralend), maar dat de klok wijder uitloopt naarmate hij tikt – een universum dat zich uitbreidt en ontwikkelt, net als een plant die in steeds grotere kringlopen groeit.

In de astronomie ontdekken we ook interessante φ-gerelateerde feiten. Bijvoorbeeld de verhouding tussen de omlooptijden van planeten of manen: niet altijd exact simpele breuken (zoals 2:1), maar soms dicht bij bijzondere waarden. De baanresonantie tussen sommige hemellichamen komt in de buurt van φ. Een voorbeeld: de planetoïdengordel heeft hiaten (Kirkwood-gaten genoemd) op posities die verband houden met φ-achtige verhoudingen van omlooptijd ten opzichte van Jupiter, alsof die verhoudingen vermijden dat er langdurig objecten blijven (instabiliteit of juist stabiliteit speelt daar een rol). En dan nog de spiraalarmen van bepaalde sterrenstelsels. Die blijken een pitch angle (de hoek waaronder de armen spiraliseren) te hebben die overeenkomt met een gulden spiraal. Een onderzoek bij het Max Planck Instituut suggereerde dat de structuur van sommige melkwegstelsels de gulden snede ratio laat zien in hun opbouw​. Alsof de natuur, op astronomische schaal, wederom uitkomt op deze verhouding als een universeel bouwprincipe – in ruimte én misschien in tijd. Zowel bij alle zonnebloemen op Aarde als bij onze zon en daar voorbij.

Ook het oude idee van de “muziek der sferen” sluit hier mooi op aan: de planeten zouden in hun bewegingen harmonieuze patronen creëren. Kepler was al overtuigd van een soort kosmische muziek verborgen in planetaire bewegingen. Als Phi hierin een rol speelt, is het misschien het mechanisme dat voorkomt dat deze “muziek” eentonig (te ordelijk) of dissonant (te chaotisch) wordt—precies zoals we eerder zagen bij plantenpatronen.
Sommige esoterische denkers verbinden Phi zelfs aan kosmische cycli zoals de astrologische tijdperken (Ram, Vissen, Waterman), of aan lange cycli zoals de precessiecyclus van ~25.920 jaar. Hoewel dit speculatief blijft, spreekt het tot de verbeelding dat Phi zelfs tijd en ruimte met elkaar verbindt in een elegant, universeel patroon.

In the Sumertime

De Sumeriërs waren een volk uit het oude Mesopotamië, bekend om hun indrukwekkende bijdragen aan de wiskunde en astronomie. Ze worden beschouwd als de uitvinders van de klok, omdat ze (voor zover we weten) als eersten de dag verdeelden in 24 uur, elk uur in 60 minuten en elke minuut in 60 seconden. De seconde was de kleinste eenheid die men toen gebruikte om twee momenten in tijd mee te meten en verbinden. Opvallend is dat ze zowel het tientallig als het zestigtallig stelsel (sexagesimaal) kenden. Net zoals onze (wereldwijde) beschaving gebruikten ze het tientallig stelsel voornamelijk voor alledaagse handel en administratie. Omdat tellen met tien vingers eenvoudig was, leert men ons hierover. Aan de andere kant van het spectrum hanteerde men het zestigtallig stelsel voor astronomische observaties en het meten van tijd en hoeken.

Maar waarom zestig? Als een volk reeds een tientallig stelsel heeft, waarom nog een zestigtallig erbij verzinnen als je ook gewoon zes keer tot tien zou kunnen tellen? Historisch gezien is dit een raadsel. De Sumeriërs hebben nergens schriftelijk toegelicht waarom ze kozen voor dit specifieke getal dat aan de basis ligt van de tijdsmeting. Moderne onderzoekers baseren hun conclusies op indirecte aanwijzingen en logische redeneringen, niet op een directe Sumerische verklaring. De klassieke opvatting is dat ze het zestigtallig stelsel voornamelijk uit praktische overwegingen gemaakt hebben. Met andere woorden: omdat het handig is dat zestig deelbaar is door veel verschillende getallen, te noemen 1, 2, 3, 4, 5, 6, 10, 12, 15, 20 en 30. Bingo! Maar of rekengemak alleen voldoende reden was om zo’n diepgewortelde keuze te verklaren, blijft onzeker.

Interessant genoeg ontdekte de wiskundige Joseph-Louis Lagrange in 1774 (opnieuw?) dat de laatste cijfers van de Fibonacci-getallen een periode van 60 hebben. Dit heet tegenwoordig een Pisano-periode (als eerbetoon vernoemd naar Leonardo Pisano, de échte naam van Leonardo Fibonacci). Zou dit een aanwijzing kunnen zijn dat de Sumeriërs intuïtief iets van deze onderliggende structuur aanvoelden of er misschien zelfs het fijne van wisten?

Links op het scherm heb ik met een animatie geprobeerd het patroon duidelijker te maken. Te zien is ieder getal van de reeks van Pisano/Fibonacci in een cirkel gezet. Wanneer we de reeks van Pisonacci één voor één aflopen dan merken we dus dat de laatste cijfers (de één-heden) zich iedere 60 getallen herhalen. Dat betekent dat de grootste wijzer van het universum zijn klokje rond is na exact zestig tikken.

Wat mogelijk opvalt bij het kijken naar de tik van de klok is de positie van de 0 en de 5. Dat vertoont opmerkelijke gemeenschappelijkheden met de klok die wij kennen, toch? De wiskunde van de Sumeriërs was van hoogstaand niveau, zou het kunnen dat ze de diepgang van de (ver)deling van de wereld om ons heen reeds hadden ontdekt en die hebben gebruikt om de klok mee op te stellen? De Phi wordt samengesteld door telkens 2 voorgaande elementen bij elkaar op te tellen, in essentie is dat niet zo ingewikkeld. Historisch gezien weten we zeker dat men wereldwijd met dit patroon bezig was, van China en Amerika tot in Europa en India werd het soms onafhankelijk van elkaar gevonden.

Voor wie het zich afvraagt, óók in de tientallen (het voorlaatste cijfer van ieder fibonacci-getal) zit een dieper herhalend patroon verscholen. Die herhalen zich om de 300 tikken, vijf keer zoveel. Dezelfde vervijfvoudiging doet zich ook voor bij de honderdtallen: die herhalen zich om de 1500 tikken. Daarna wordt iedere cyclus tien keer hoger in plaats van vijf. Een intrigerende opbouw die ongetwijfeld vele onderliggende patronen bevat waar we nu langsheen kijken.

In essentie symboliseert Phi in de context van een kosmische klok het idee dat de tijd zelf structureel verbonden is met ruimte en vorm. Net zoals φ de verbinding was tussen het deel en het geheel in de ruimte, zo zou φ ook de verbinding kunnen zijn tussen cycli op verschillende tijdschalen – het kleinste moment en het grootste tijdperk verbonden door een gouden draad. Of dit letterlijk zo is en of de Sumeriërs dit allemaal reeds wisten, is minder belangrijk dan wat het ons zegt: dat er een diepe samenhang bestaat in hoe het universum zich afwikkelt. Het toont ons dat we ons begeven in een wonderlijke wereld waar onze ogen en zintuigen maar amper voor zijn uitgerust.

Conclusie: eenheid in verscheidenheid

We zijn aan het eind gekomen van deze eerste verkenningstocht in de wereld van Phi. We begonnen bij een eenvoudige lijnverhouding en eindigden bij grootse ideeën over een kosmische klok – en daartussen hebben we gezien hoe één getal een verbazingwekkend spectrum aan verbindingen legt. Phi, de gulden snede, staat symbool voor eenheid in verscheidenheid: het Ene dat zich trouw toont in elk verdeeld deel. In wiskundige zin zagen we dat in de zelfgelijke verdeling van een lijnstuk en in de Fibonacci-getallen. In de natuur zagen we het in spiraalvormige groeipatronen die efficiëntie en schoonheid geven op het randje van chaos en orde. In bewustzijn en esthetiek proefden we het idee dat onze geest misschien resoneert met deze verhouding, wat harmonie en schoonheid voor ons definieert. Historisch bleek dat Phi een verborgen schat was die mystici, architecten en denkers inspireerde – van piramidebouwers en Pythagoreeërs tot Renaissancekunstenaars. En zelfs in de ritmes van planeten en de metaforen van tijd konden we echo’s van φ terugvinden.

Wat maakt Phi nu zo fundamenteel? Misschien omdat het ons herinnert aan het idee dat alles met alles verbonden is. Wanneer we een zonnebloem bestuderen, een middeleeuws kunstwerk bewonderen of in de nachtelijke hemel de spiraal van Andromeda zien, ervaren we intuïtief een samenhang. Phi is als een gouden sleutel die één van de sloten van dit mysterie opent: het toont een mechanisme (proportie) waardoor het grote en het kleine op elkaar afgestemd blijven. Het is alsof de natuur, door Phi te gebruiken, ervoor zorgt dat wanneer iets groeit of zich ontwikkelt, het nooit de band met het geheel verliest. Dat is een troostrijke gedachte: in de wanorde van verandering is er een lijn van orde die alles bijeenhoudt.

In de volgende artikelen van deze reeks zullen we nog dieper graven. Een oude spreuk luidt: “Wie de eenheid ziet, begrijpt de veelheid.” Phi laat ons eenheid zien in de taal van de veelheid van vormen. Het nodigt ons uit om met verwondering te kijken naar de wereld en te erkennen dat er orde is in de schijnbare chaos, verbondenheid in ogenschijnlijk losse delen. Dat chaos nimmer willekeur is. Misschien is dat wel de diepste boodschap van dit kostbare juweel van de geometrie: dat de wereld één is, en dat één zich uitdrukt in de wereld – in gulden verhouding, met een gouden randje...